正三角形、菱形、正六面體...這三個東西是「等軸測視頻圖形遊戲」的基礎技術。

這種製作圖像的策略風格早期又被稱為「2.5D」或「偽3D」，（跟後來的Doom相比，這真的是偽3D。）

它最大的優勢是「利用平行投影技術讓一張像素圖盡可能展現物件的多個面向給玩家」，會給玩家一種生動活潑的感覺，（而不是錯覺般的立體感！玩家喜歡的終究是「生動活潑」。這也是為什麼隨著儲存空間變得越來越便宜、製作像素圖成本越來越低後，2D遊戲又漸漸地回頭在遊戲市場佔有一席之地的原因，——因為2D遊戲又變得更加生動活潑了。）

同時，這技術經常是「日系RPG」和「歐美RPG」最關鍵的分水嶺。（日系主要是回合制戰棋戰略遊戲會使用這種技術。）
這些年，像素與復古風遊戲又開始盛行，製作這樣的遊戲好像變成一種顯學，如何製作這種風格遊戲的討論與「教學」忽然變多了！
但怎麼製作美術是一回事，這裡講的是程式。

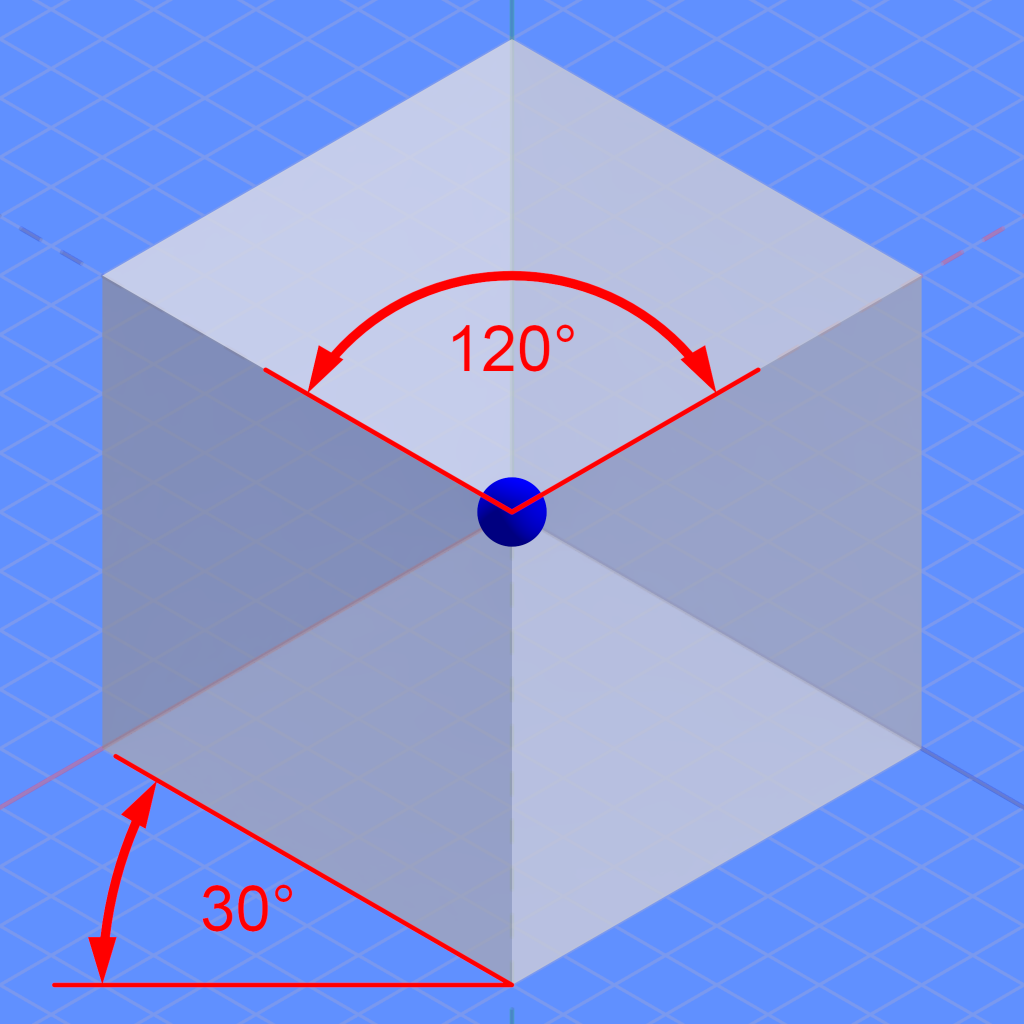
實務上，製作時用的並不是「正六角形」，而是下圖這種略扁的六角形。

為什麼？因為數學運算上比較容易。

正六邊形的寬高比是「一比根號三」，如何表達和計算根號三不是件容易輕鬆的事。
雖然近代電玩程式大神約翰卡馬克有教大家「用1.41423表示根號三」這樣簡單的數學技巧，但如果能夠連這樣的步驟都省去豈不是更好。
所以...把兩種六邊形擺在一起看可能會比較好解釋為什麼不採用正六邊形。

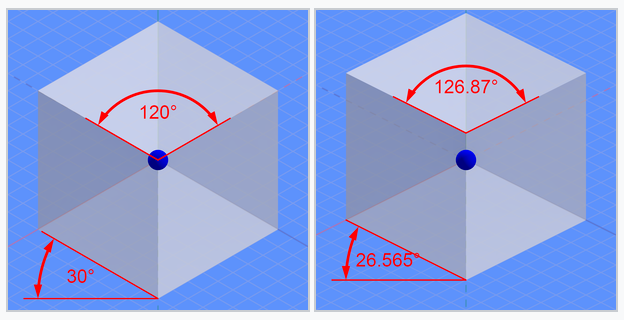
1.圖像（例如人物）內容的大小其實不需要修改，只是記得在一張正方形的作圖範圍內，內容的高度不要超過三分之二，然後將內容的重心略微提高即可應用在兩種不同系統了。
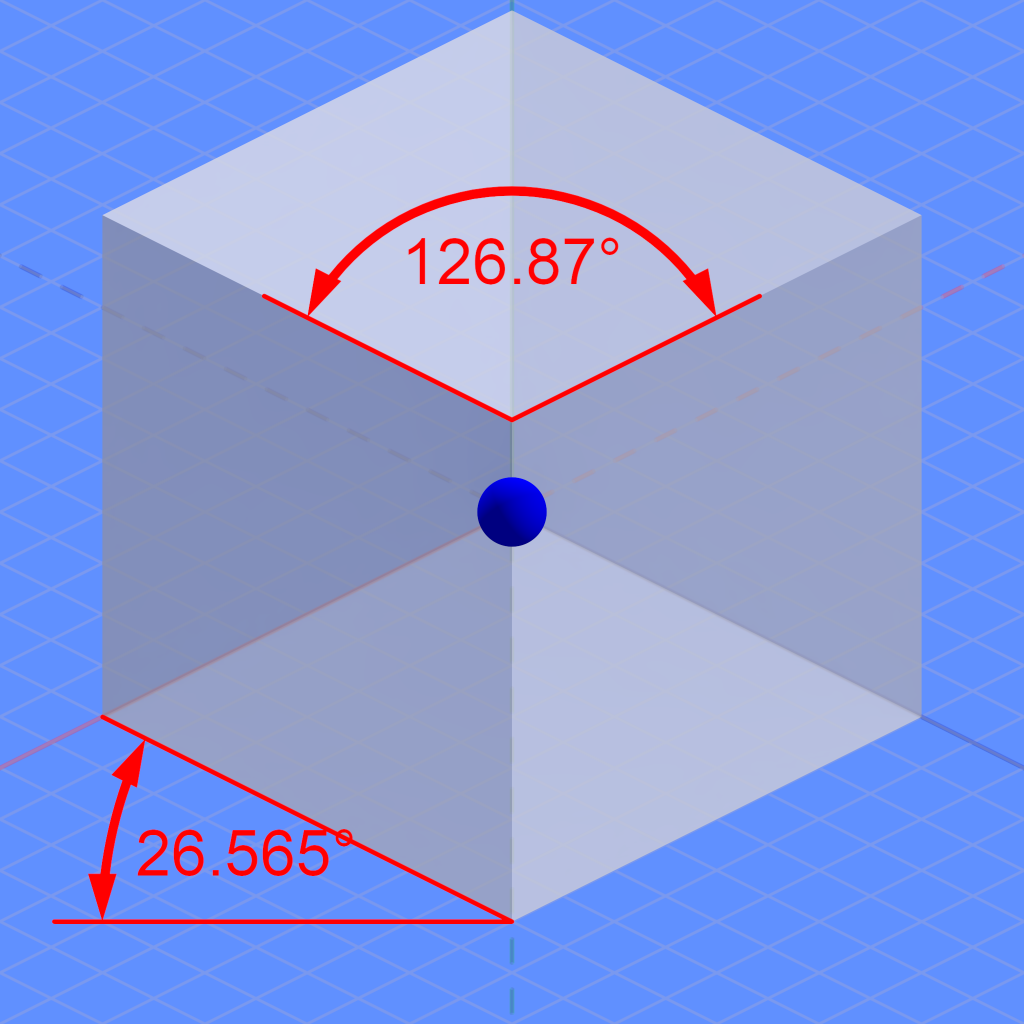
2.正六邊形為六個正三角形構成，但略扁的三角形其實是四個「底高為一比ㄧ」的三角形和兩個梯形構成。如果仔細看會發現「它們仍舊使用同一個中心」。

如果底是由兩個「底高為一比ㄧ」的三角形所構成，就可以用一個「長寬為一比二」的長方形去做定位的預估。
計算一個「一比二根號三」的長方形容易？還是「一比二」的長方形容易？
這已經不只是效能問題了，就連程式碼編寫維護的輕鬆程度可是天差地遠。

所以在實務上，在無數個「長寬為一比二」的長方形堆疊起來的遊戲世界中，每個長方形的上寬中間作為圖像的中心點定錨，就可以快速地「用正六邊形構造圖像」「用略扁的六邊形跑程式」。

（不過，說「這是實務」，那是以前，兩種系統的圖像不可能完美轉換，只是偏差值很小。如果可以，還是請直接以略扁的六邊形去做圖像製作。）

如何製作菱形呢？

    final path = Path();

    // 定義菱形的四個頂點
    final vertices = [
      Offset(0, -height/2),
      Offset(width/2, 0),
      Offset(0, height/2),
      Offset(-width/2, 0),// 左頂點
    ];

    // 從上頂點開始
    path.moveTo(vertices[0].dx, vertices[0].dy);

    // 連接其他頂點
    for (int i = 1; i < vertices.length; i++) {
      path.lineTo(vertices[i].dx, vertices[i].dy);
    }

    // 連接到起始點，形成一個封閉的形狀
    path.close();

    // 繪製菱形
    canvas.drawPath(path, Paint()..color = Color(0xFF0000)..style = PaintingStyle.stroke);

這是Canvas繪圖的部分。

但作為一個BodyComponent，必須要設定為菱形，否則碰撞的結果會不正確。

    final shape = PolygonShape();
    final vertices = [
      Vector2(0, -height/2),
      Vector2(width/2, 0),
      Vector2(0, height/2),
      Vector2(-width/2, 0),
    ];
    shape.set(vertices);

（接下來還有六角形。但其實就是數學計算而已，作法跟上面菱形一樣，只是數學不一樣而已。）